効用最大化とは?-公務員試験ミクロ経済学
あっ、先輩、こんにちは...。
こんにちは、カズ。どうしたの?そんなに暗い表情で。
今月お金が残り1,000円しかなかったのに、衝動的にマンガ2冊買ってしまいました。チョコレートも食べたかったので、お金残しておけば良かったと今になって後悔しています…。
なるほど。じゃあ今回のカズは、限られた予算の中で効用を最大にできなかったってわけでね。
「効用」を「最大」ってどういうことですか?
うん、経済学では限られた予算の中で満足度(=効用)を一番高くすることを「効用最大化」と言うよ。公務員試験では基本中の基本だからしっかりと理解できるようにしよう!
効用最大化とは?
ミクロ経済学は、限られた資源(=モノ、カネ、労働など)の中で企業にとっては利潤、消費者にとっては満足度(=効用)を高めるにはどのような選択をするべきかということを考える学問です。
消費者の満足度に関する分析をする際には、「予算」という制約と「効用」という主観的な満足度の2つが分析の際に用いられます。「予算」の中で「効用」を最も高くできる財・サービスの消費の組合せを「効用最大化」、あるいは「最適消費」と言います。
効用曲線とは?
「効用」は、「効用曲線(無差別曲線)」と呼ばれるグラフや、効用関数と呼ばれる計算式を使って分析します。
消費者が消費する財を2財のみとした場合、一般的な「効用曲線(無差別曲線)」は、下記のように原点に対して凸の曲線になります。また、「効用曲線」は無数に描け、原点から遠く離れた「効用曲線」ほど効用が高くなるとされます。
図;2財の効用曲線
普通の消費者であれば、自分の効用(満足度)を出来る限り高めたいと思います。つまり、2つの財をより多く購入・消費出来れば効用も高まります(原点から遠く離れた効用曲線上にある消費の組み合わせは効用が高くなります)。
例えば、「お茶2本、コーヒー2本」の組み合わせより、「お茶3本、コーヒー3本」の組み合わせの方が効用は高くなります。そのため、「お茶2本、コーヒー2本」の組み合わせと「お茶3本、コーヒー3本」の組み合わせはそれぞれ効用の大きさが違うため、違う効用曲線に属することになります。
逆に、「お茶4本、コーヒー1本」の組み合わせと「お茶2本、コーヒー2本」の組合せは同じ効用曲線上のあるため、どちらの組み合わせであっても効用自体は同じと言えます。
bestkateikyoshi.hatenablog.com
予算制約線とは?
効用を高くするためには財をたくさん消費すればいいということになりますが、現実社会では、消費者は個々の貯蓄の中で財を購入するため、購入できる財の数量にも限界があります。そこで、予算制約式や予算制約線を用いて、予算内で効用を最大にできるような財の組み合わせを検討します。
図;予算制約線
例えば、1,000円しか予算がない状況で、1個250円のチョコレートと1冊500円のマンガをどう購入するかという消費の組み合わせを考えた時、上記の図のように9つの青い点しか購入パターンはありません。
この時、消費できる数量の限界(予算1,000円ピッタリの組み合わせ)を結んだ線を予算制約線と言います。そして、予算制約線から原点を含む左側の領域を消費可能領域と言います。この消費可能領域の中で消費者は効用最大化を目指すことになります。
bestkateikyoshi.hatenablog.com
効用最大化点はどこになる?
効用が最大になる消費の組み合わせは、消費可能領域の中で、原点から一番遠い効用曲線を通る消費の組み合わせになります。この時、下記のような図の場合、以下のように予算制約線と効用曲線の接点が効用最大となります。
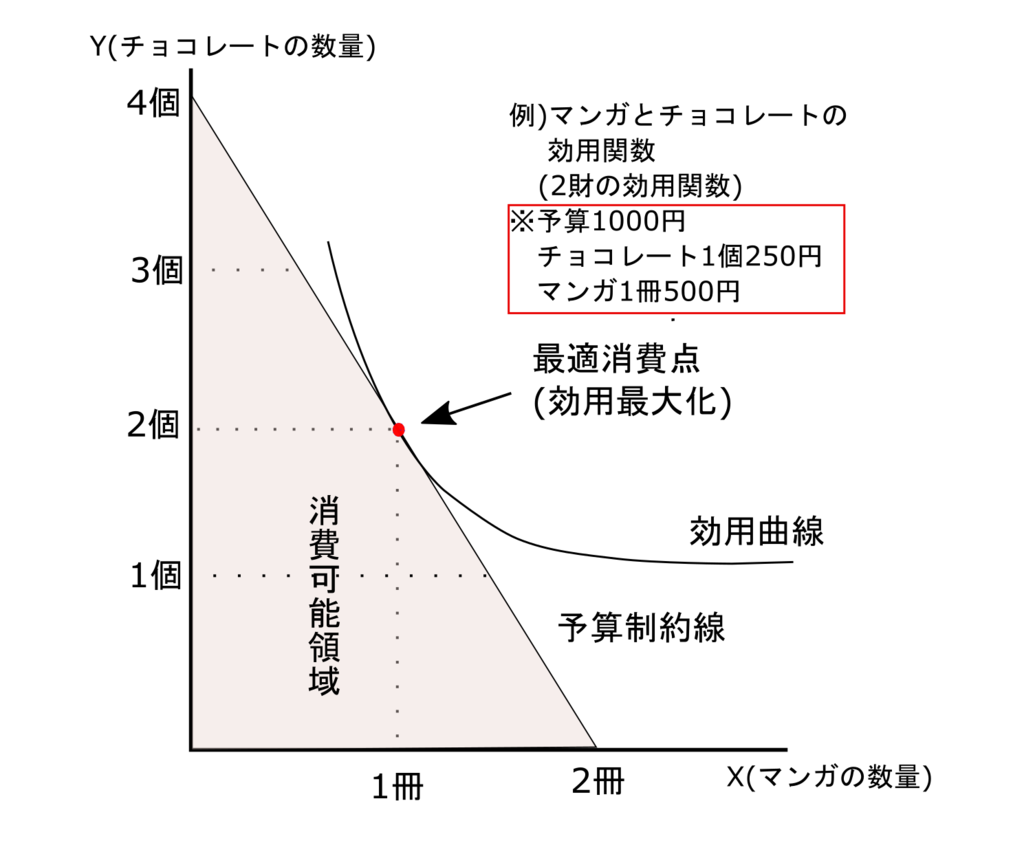
なぜ予算制約線と効用曲線の接点が効用最大になるかですが、他の効用曲線と比べてみると分かりやすいかと思います。
図;最適消費(効用最大化)
上記の図のように、効用曲線を右上にスライドさせていくと、最終的に予算内で消費できる組み合わせを持つ効用曲線は予算制約線と効用曲線の接点になります。そのため、「チョコレート0個、マンガ2冊」や「チョコレート1個、マンガ1冊」の組み合わせよりも「チョコレート2個、マンガ1冊」の方が効用は高く、この組み合わせ以上に予算内で効用が高いものはないため、これが図上の「効用最大化」となります。