短期の総費用曲線(TC)と総収入関数(TR)の求め方と利潤最大化は?-公務員試験ミクロ経済学
こんにちは、先輩。あ、ちょっと聞きたいことがあるのですが。
こんにちは、カズ。どうしたの?
先週のミクロ経済学の授業で「短期生産関数」と「短期費用関数」についてやったのですが、今日の授業では「総費用関数」と「総収入関数」が出てきました。なんか全部同じように見えて訳が分からなくなってます…。
なるほど、確かにミクロ経済学では似たようなグラフがたくさんあって初めは混乱するよね。でも、どうして「総費用関数」と「総収入関数」がでてくるのか?という「なぜ?」を理解すれば違いが理解できるようになるから今日はしっかりと理解してしまおう!
「短期生産関数」と「短期費用関数」とは
まず、「短期生産関数」と「短期費用関数」は以下のように、縦軸をそれぞれ「生産量」、「総費用」で、横軸はどちらとも「労働投入量」をとる図に表します。


「短期生産関数」と「短期費用関数」については、こちらのページで詳しく説明があるので、見て頂ければと思います!
「総費用関数」とは?
総費用TCは、「短期費用関数」で出てきた「労働投入量L」と「資本投入量K」にかかる費用の合計で同じです。しかし、大きく違うポイントとしては、グラフの縦軸、横軸にとる値になります。
「総費用曲線」では、グラフの縦軸を「総費用(TC)」、横軸を「生産量(Y)」で考えることになります。例えば、先ほどの「短期生産関数」と「短期費用関数」のグラフを例にするとき、この2つの図を使って1つの図の中に「総費用曲線」を導出することが出来ます。


まず横軸の共通する「労働投入量」部分を見てください。労働投入量が5人の時、生産量(Y)は10台で、総費用(TC)は1,500万円となります。次に、労働投入量が10人の時、生産量(Y)は20台で、費用(TC)は2,000万円になります。
このように、短期生産関数の図と短期費用関数の図の「総費用(TC)」と「生産量」をグラフの縦軸と横軸に置いて表したグラフが以下のように総費用曲線になります。
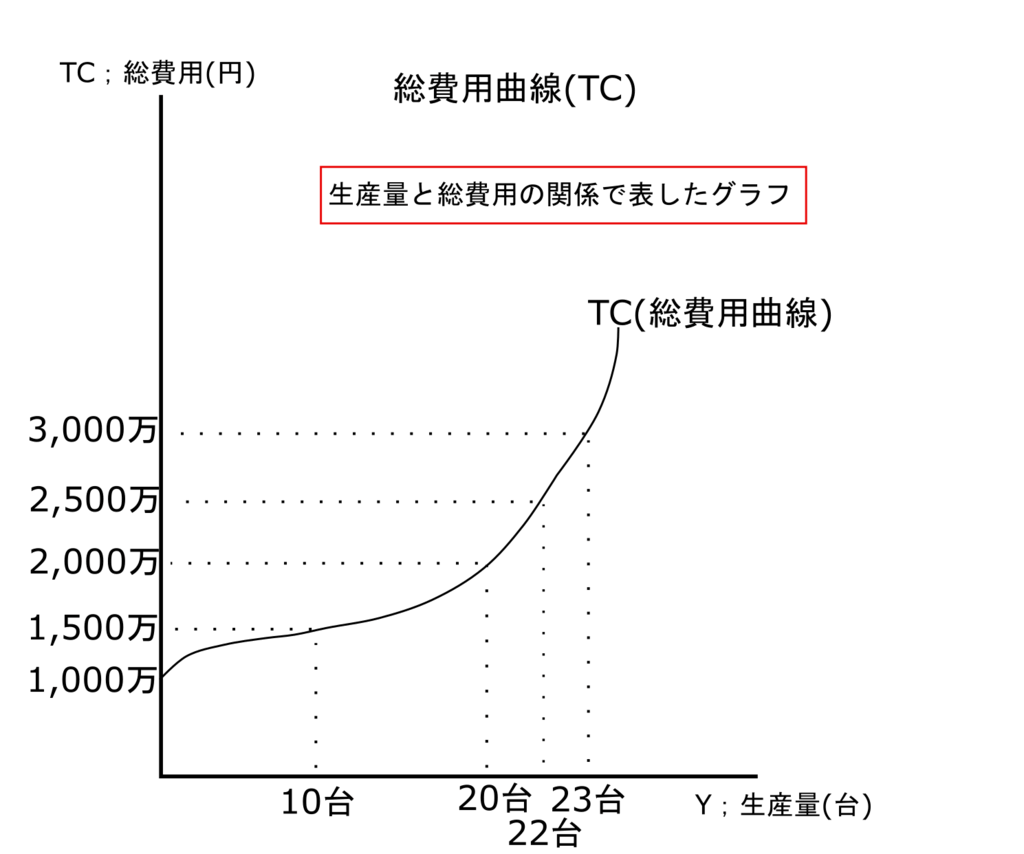
「総費用曲線」は、労働投入量を多く増やしすぎても資本投入量が固定のため、ある一定の生産量を超えると短期では生産量は増えなくなり、逆に総費用だけが増えてしまうことになりため、上記のようなグラフの形をとります。
繰り返しになりますが、「総費用曲線」は「短期生産関数」と「短期費用関数」を基に曲線を作ることができ、違いとしては縦軸、横軸のとる値になります。
「総収入関数」とは?
企業の最適生産量を分析するためには、「総費用曲線」だけでは足りません。そこでもう一つ「総収入関数TR(Total Revenue)」も必要になってきます。
まずそもそも収入とは、生産物を売った時に得た売上金額のことで、例えば、ある自動車工場では自動車1台を150万円で販売しているとし、縦軸を「総収入(TR)」、横軸を「生産量(Y)」としたとき、総収入曲線は以下のようになります。
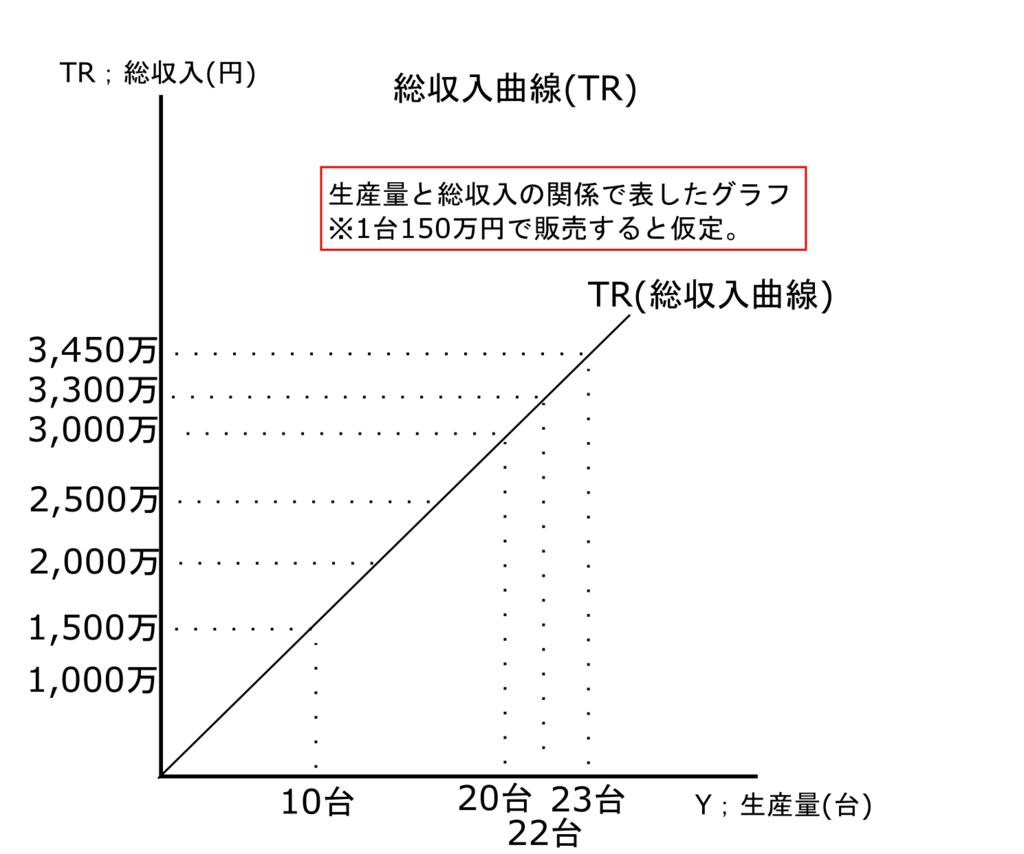
10台生産して全て販売できたとすると1,500万円収入を得られ、20台生産すると3,000万円収入を得られるという感じです。
利潤を求めるには?
利潤とは、企業の儲けのことを言い、「総収入から総費用を引いた残ったお金」。ミクロ経済学では、企業は利潤を最大化するために最適な生産量を求めます。先ほど、「総費用曲線」と「総収入関数」をグラフで表しましたが、これらを同じグラフの中に表すと、以下のようになります。
図:総費用曲線と総収入関数から利潤を求める方法
図のように、総収入関数が総費用曲線を上回っている生産量では、利潤が発生しているということを表しています。このグラフを見ると、どの生産量で利潤が一番大きいか(総収入関数と総費用曲線との開きが一番大きいか)が視覚的に分かります。
短期費用では企業の最適な生産量をこのようなグラフを使って分析できます。もちろん、実際に問題を解くときには計算など必要になってきますが、まずは視覚的にイメージできることが大切です。