価格が異なる場合の需要の価格弾力性-公務員試験ミクロ経済学
あっ、先輩、こんにちは!以前、「需要の価格弾力性」についての基本を教えて頂いたと思うのですが、その時に、同じ商品でも元の価格によって「需要の価格弾力性」が違うことがあるって言ってましたよね?あれってどういうことですか?
こんにちは、カズ。そうだね。じゃあ今日は「需要の価格弾力性」について少し復習をしながら勉強していこう!
需要の価格弾力性とは?
「需要の価格弾力性」は「価格が1%変化した時に需要量が何%変化するか」を指します。公務員試験では頻出の分野で、弾力性を求める公式はよく使うことになります。
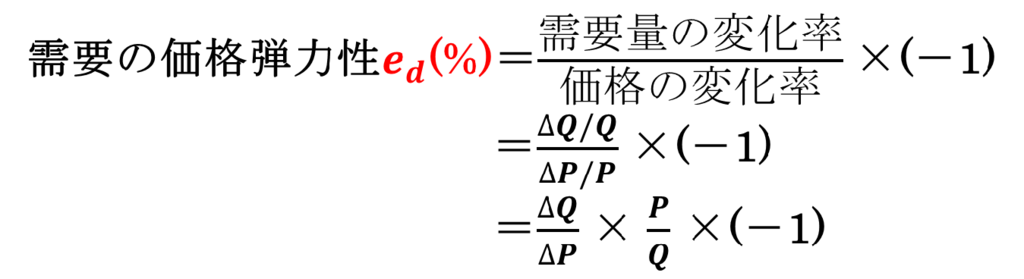
△Q/△Pは需要曲線y=ax+bの傾きaの逆数
P,Qは元々の(基準となる)価格と数量
例えば、当初1個2,000円のケーキがあるとした場合、ケーキの需要の価格弾力性は4となります(ケーキの需要曲線y=-5x+2500としたとき)。
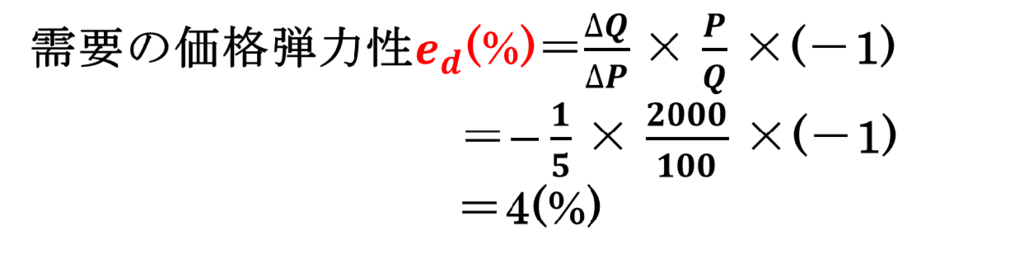

価格が2,000円でも需要曲線の形状の異なる別の財、例えば専門書の場合、専門書の需要の価格弾力性は4/3となります(参考書の需要曲線はy=-15x+3500としたとき)。
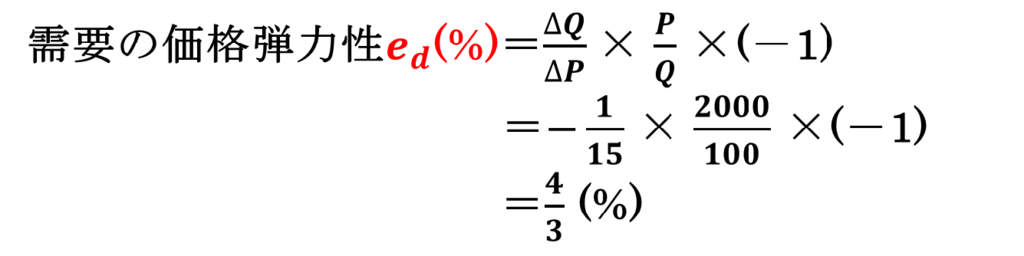
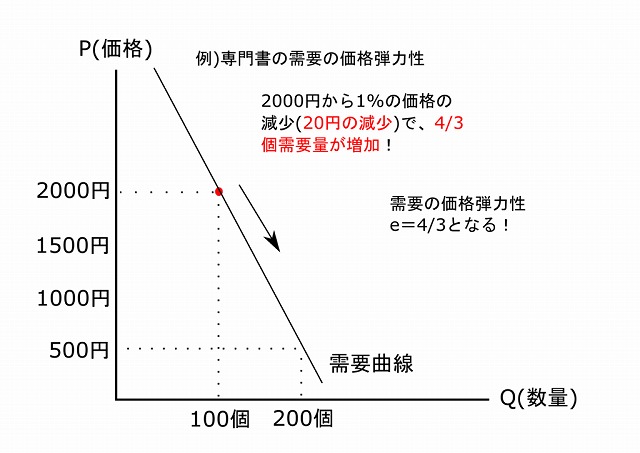
同じ財でも価格が異なるときの需要の価格弾力性は?
需要曲線が同じ形状でなければ、需要の価格弾力性が異なることは理解できたと思います。しかしながら、同じ財でも元の価格が異なると需要の価格弾力性が異なることがあります。先ほどのケーキの需要曲線を使って見てみましょう。
もともと1個2,000円のケーキがあるとした場合は、下記のようにケーキの需要の価格弾力性は4となりました。
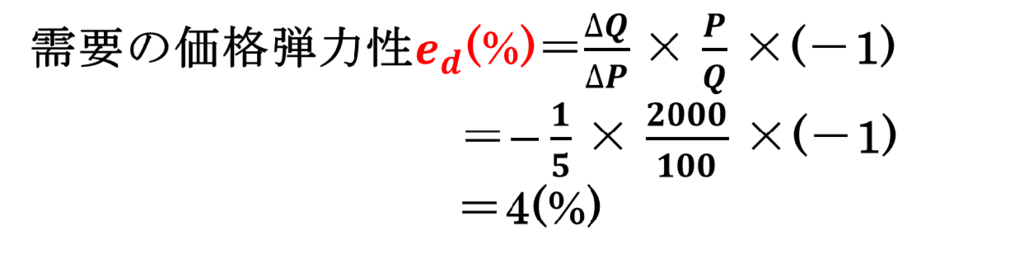

次に、1個の価格が1,500円の場合には、以下のように需要の価格弾力性を導出することができます。


公式の△Q/△Pの部分に需要曲線の傾きの逆数-1/5を当てはめるのは、1個2,000円の時と同じです。しかしながら、公式の中の価格Pと数量Qの部分には、Pに1,500円、Qに200個を入れて計算することになります。その結果、価格が1,500円の時の需要の価格弾力性は3/2%になり、2,000円の時の需要の価格弾力性4%よりも小さくなります。
これは1,500円から価格が1%(15円)下がった時に、需要量は3/2%増加するということを表しています。価格が1,500円の時の需要量は200個のため、200個の3/2%(=1.5%)は、200(個)×1.5÷100=3(個)となります。つまり、元の価格が1,500円の時は価格が1%下がったら3(個)需要が増加するということになります。
このように、もともとの価格が異なると需要の価格弾力性も異なってきます。ただし、ここで理解しておきたいことは、元の価格が1,500円の時でも、20円下がった時(2,000円の1%)の需要量が4個増えるのは同じだということです。
つまり、一定額の値引きに対する需要の増加量はいつでも同じですが、それを「元の価格から1%下がった時」とすると、元の価格は2,000円だったり1,500円だったりと異なるため、1%も20円や15円と異なってきます。
ちなみに、需要曲線が直角双曲線の際には、需要の価格弾力性は元の価格によって変わらず、元の価格がどの価格でも需要の価格弾力性は1になるので注意が必要です。
最後に、ケーキの需要曲線を使って、元の価格が1,000円の時の需要の価格弾力性も求めてみたいと思います。

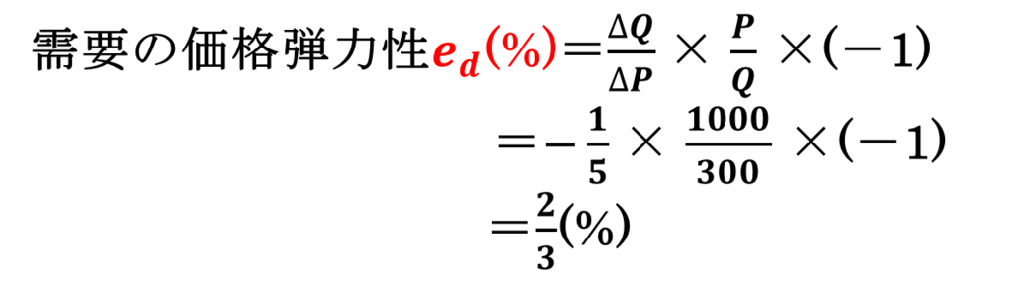
このように、元の価格が1,000円の時の需要の価格弾力性は2/3%になります。つまり、価格が1,000円の時の元々の需要量は300個のため、300×2/3÷100(0.666%)となり、1%の価格減少(10円の減少)で需要量2個が増加するということになります。
bestkateikyoshi.hatenablog.com