異時点間の消費理論とは?-公務員試験マクロ経済学
あっ、先輩、こんにちは!先輩はもう就活の時期ですよね。どんな業種の面接受けるとかもう決まったりしているのですか?
うーん、業種とかはあまり絞ってないけど、給料が高いところがいいかな。将来のために貯金したいし。
確かに年金とか将来の不安も多いので僕も稼げるうちに稼ぎたいですね。
そうだよねー。そういえば、ミクロ経済学でも消費者を分析する理論の中に「異時点間の最適消費理論」という理論があって、若い時と老後の2つの時期に分けて、一生を通じてどのように効用を最大にするかって分野があるよ。公務員試験でもよく出てくるから、公務員試験受けるとしたらしっかりと覚えておいた方がいいよ!
異時点間の消費とは?
公務員試験では、2つの財の効用が最大となる消費量の組み合わせを考える2財モデルというものがよく出題されます。例えば、「チョコレート」と「ケーキ」のように2財を使って分析が行われますが、一生を「若年期の消費金額」と「老年期の消費金額」に分けて、効用の分析が行われることがあります。
これを「異時点間の消費」と呼ぶのですが、土台となる考え方は通常の2財モデルとほとんど変わりません。少し異なってくるのは、以下のようなルールが設定される点になります。
[異時点間の消費条件例]
・消費する期間を若年期、老年期の二期間に分ける
・若年期に合計1億円稼ぐものとする
・老年期には年金などを受給せず、収入はないものとする
・老年期には若年期に貯蓄しておいたお金を全て消費に使い切るものとする
・若年期に残したお金は全て銀行などに預けており、利子率分増えて還ってくるものとする
・銀行に預けた際の利子率は10%とする
※1,000万円預けたとすると老年期に1,100万円になって還ってくる
上記の条件は一例なので、問題によって利子率が違ったり、若年期に稼ぐ金額が違ってきたりします。ただ、大きなポイントとしては、「予算制約線は若年期に稼いだ金額と貯蓄した金額によって変化する」という点です。また、若年期に貯蓄/借入した金額によって利子率分老年期の保有金額が増減するため、この点が通常の2財モデルと大きく異なる部分になります。
例えば、若年期に稼いだ1億円のうち5,000万円を若年期に使って、残りの5,000万円を貯蓄したら、利子率10%分老年期に増えるため、この人の一生で使えるお金(予算)は1億500万円になります。
このように、貯蓄をたくさんすればするほど利子収入が増えるので、「若年期の1億円を全て預金すると効用は高くなるんじゃない?」と思う人もいるかもしれません。しかしながら、若年期に生きていくためにはお金が必要なので、バランスよくお金を使うことによって効用を高めることができます。

もし消費金額の組み合わせを(若年期の消費金額、老年期の消費金額)=(0, 1億1千万)とすると、効用曲線は上記の図になります。この状態だと予算制約の中で、もっと効用曲線を右上にシフトすることができるので、あまり良い消費の組み合わせではありません。
効用最大化となる最適消費点は、予算制約線と効用曲線が接する部分になるので、下記の図のように効用曲線を右上にシフトさせていくと、どこが最適消費点の消費金額の配分になるのか分かります。
図:異時点間の消費の最適消費点①
このように、もともと若年期で1億円しか稼いでなかったけど、6,000万円を老年期のために銀行預けたことで6,600万円になるため、一生で使える金額の合計は1億600万円になります。

異時点間の消費理論における利子率の変化
最後に、公務員試験で出題される利子率が変化したときのパターンについて、グラフを使って紹介していきたいと思います。
利子率が変化するパターンとは、「予算制約線の傾きが変化して、一生で使える金額が変化する」パターンを言います。
例えば、銀行に預けるよりも、ある企業に投資した方がリターン(/収益率)が大きくなることが判明したとします。そのリターンが20%としたとき(例えば投資額100万円によって20万円がリターンとして返ってくるとしたとき)、「予算制約線」の傾きは下記のように急になります。
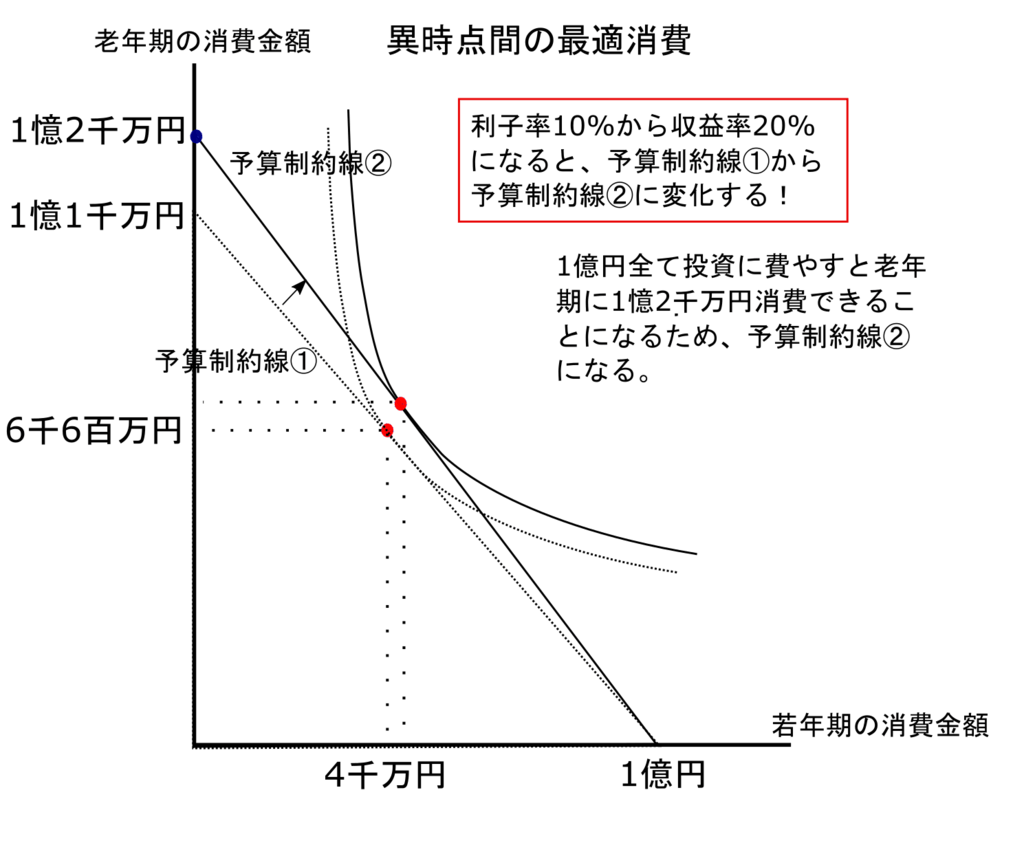
なぜ傾きが急になるかというと、もし若年期に1円も費やさなかったとしたら老年期に1億2千万円費やせることになるように、収益率が増加することによって一生に使える金額がその分増える可能性があるからです。図の予算制約線の青い点(若年期の消費金額、老年期の消費金額)=(0, 1億2千万)からも分かると思います。このような利子率/収益率の変化後の効用最大化となる組み合わせを求めさせる問題もよく出題されるので、しっかりと原理を理解しておくことが重要になります!
最後に
今回紹介したパターン以外にも、①若年期にお金を逆に銀行から借りるパターン(利子分多く返すため一生で使える金額減るパターン)や、利子率が減少するパターン(予算制約線の傾きが緩やかになるパターン)などがあります。
しっかりと原理を覚えることで他のパターンにも対応できるようになるので、グラフをみて理解できるようにしましょう!