ソロー=スワン・モデルとは?-公務員試験マクロ経済学
こんにちは、先輩。先日経済成長理論の範囲で「ハロッド=ドーマー・モデル」というモデルを勉強しましたが、今日の講義で今度は「ソロー=スワン・モデル」というのが出てきました。両者の違いが全く分からないのですが、教えて頂けないでしょうか…。
こんにちは、カズ。マクロ経済学では経済成長理論で「ハロッド=ドーマー・モデル」と「ソロー=スワン・モデル」の2つ勉強しないといけないから確かに大変だよね。
そうなんですよ、2つの計算式見てるとどっちがどっちだか分からなくなってきます。
そうだね。公務員試験で「ソロー=スワン・モデル」は、「ハロッド=ドーマー・モデル」と比べると出題頻度は低いようだけど、でもやっぱりもし出題されたときに対応できなかったら勿体無いから、今日は「ソロー=スワン・モデル」について理解できるようにしていこう!
ハロッド=ドーマー・モデルとの違い
まず、ハロッド=ドーマー・モデルでは、資本Kと労働Lという2つの生産要素をそれぞれどのくらい投入するとどれだけ生産量、つまり国民所得が増加するのかモデルを使って分析しました。ハロッド=ドーマー・モデルでは、資本Kと労働Lという2つの生産要素をバランスよく投入することによって生産量が増加する、非代替的なモデルを想定していました。非代替的とは、一方の生産要素が他の生産要素を代替しないということを表しており、例えば資本Kの代わりに労働Lをたくさん増やしても生産量は増加しないという立場に立っていました。
一方、今回学習するソロー=スワン・モデルでも、生産要素は資本Kと労働Lの2つを用いて考えるため、その点はハロッド=ドーマー・モデルと同じになります。しかし異なる点は、資本Kと労働Lが代替的であるという点です。例として、農業を考えてみてください。新興国では、機械ではなく、手作業で農業を行っている地域も多くあります。その場合、多くの労働力を投入することになりますが、もし資本、即ち機械を導入したらどうなるでしょうか?手作業の部分が減らすこともできるため、効率性も上がりますし、労働者を減らすこともできると思います。このように、資本Kと労働Lが代替できるという前提に立つのが、ソロー=スワン・モデルになります。
ソロー=スワン・モデルの生産関数
ここまで、ソロー=スワン・モデルでは、資本Kと労働Lは代替できるということを説明しましたが、この時、生産関数は以下のように定義されます。


ソロー=スワン・モデルの生産算数は、2つ目のコブ=ダグラス型生産関数となります。この関数は、縦軸に資本K、横軸に労働Lをとる図において、右下がりの曲線となります。ハロッド=ドーマー・モデルの生産関数はレオンチェフ型生産関数だったのでL字型の生産関数でしたが、ソロー=スワン・モデルの生産算数は右下がりの曲線となります。これは、資本Kと労働Lが代替的であるためです。

コブ=ダグラス型生産関数の式はべき乗の式になっているため、なんだか難しそうに感じてしまいますが、公務員試験ではY=F(K,L)を使うので、ひとまず安心してください。
ソロー=スワン・モデルの定常状態
それではここから実際に、公務員試験で対応できるようソロー=スワン・モデルにおける定常状態、つまり最適成長となるための方程式の導出方法を見ていきたいと思います。ソロー=スワン・モデルの問題を解くためには、これから説明する計算の過程を理解しておくのが大切になります。
まずソロー=スワン・モデルでは、Y=F(K,L)から一人当たりの生産関数を導出します。一人当たりとは、「労働人口一人当たりの生産関数」のことを言い、生産関数Y=F(K,L)を労働Lで割ります。


すると、上記のようになります。この時、一人当たり国民所得Y/Lをyとし、資本・労働比率K/Lをkとすると、y=f(k)と表すことができます。
次に、資本・労働比率k=K/Lを変化率表示の式にします。すると、△k/k=△K/K-△L/Lとなります。なぜこのように式を変形できるかですが、この部分は数学の範疇になるので、興味がある方はネットなどで調べてください。ともかく、△k/k=△K/K-△L/Lとなりましたが、ここから以下の式をそれぞれ代入します。


一つ目の式△K=~は、財市場の均衡条件等を使って導出したものになります。まず資本Kの変化分△Kは、今期の投資量となるのでIと等しくなり、財市場の均衡条件より投資Iは貯蓄S=sYと等しくなります。国民所得Yは今後の計算のために一人当たり生産関数y=f(K)に直すために、L/Lを式に挿入して、△K=s・f(k)・Lの形にします。
二つ目の△L/L=nにおいて、労働人口成長率nを表します。これら2つの式を△k/k=△K/K-△L/Lに代入すると、以下のようになります。

この時、(s・f(k)・L)/Kにおいて、資本・労働比率k=K/Lの逆数であるL/Kがあるので、L/K=1/kを代入すると、以下のようになります。

最後に、両辺に資本・労働比率kをかけると以下のようになり、これがソロー=スワン・モデルにおける経済成長の基本方程式となります。この基本方程式が成り立つ時には、最適な成長が維持できているとされ、定常状態であるといえます。

政府の介入の不要となる理由は?
ハロッド=ドーマー・モデルでは、一度現実の経済成長率Gと保証成長率Gwが乖離してしまうと、自律的に経済は安定しないため、政府の介入が必要だという考え方をとっています。しかし一方で、ソロー=スワン・モデルにおいては、政府の介入は不要としています。
まず、前提としてソロー=スワン・モデルにおいて定常状態の時には、資本・労働比率k*=K/Lはゼロと考えます。つまり、ソロー=スワン・モデルの基本方程式の中で出てきた貯蓄率sや労働人口成長率nが変化して資本K又は労働人口Lが変化したとしても、もう一方が同じに変化するため、資本・労働比率k=K/Lは一定に保たれます・。資本・労働比率kがゼロとした時、先ほどの基本方程式は以下のようになります。

上記の式をさらに、以下のように整理します。
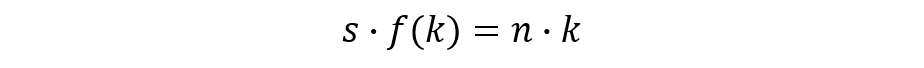
縦軸に一人当たり国民所得y、横軸に資本・労働比率kをとる図において、定常状態は交点Aとなります。

ソロー=スワン・モデルでは、上記の均衡点Aでない場合でも、政府の介入なしに均衡点A、つまり基本方程式②における左辺s・f(k)と右辺n・kがイコールになる部分で落ち着きます。
はじめに、定常状態における資本・労働比率k*に比べ小さい値をとるk₁の場合を考えます。この時、当初の資本・労働比率k₁をk*となるよう増加させます。この時、基本方程式②において、両辺に資本・労働比率kがあるため、左辺s・f(k)と右辺n・kはともに増加します。そして、最適成長水準であるk*の部分まで来ると均衡します。ハロッド=ドーマー・モデルでは投資を変化させることで不均衡が助長されてしまいましたが、ソロー=スワン・モデルでは、貯蓄率sと労働人口成長率nが一定の下で資本Kの増加により資本・労働比率kが上昇するため、均衡します。このように、自律的に定常状態を達成できるため政府の介入は不要とされています。
最後に
ソロー=スワン・モデルでは、最適な経済成長率は、労働人口成長率nの変化や貯蓄率sの変化によって変化します。労働人口成長率nの変化や貯蓄率sの変化によって先ほどの図において曲線がシフトするためです。
択一問題では、ハロッド=ドーマー・モデルとの比較で出題されることが多いので、以下のページでハロッド=ドーマー・モデルの紹介をしているので違いを理解できるようにしてみて下さい!