ローレンツ曲線・ジニ係数-公務員試験財政学
先輩、この間公務員試験の模試を受けたら、ジニ係数という用語が選択肢に出てきたのですが、ジニ係数って何なのですか?
こんにちは、カズ。あれ、ジニ係数って今まで聞いたこともない?結構ニュースや大学の授業でも出てくることあると思うけど。
はい、聞いたこと自体はあるのですが、あんまり内容は理解していません…。確か貧富の格差に関するものでしたっけ?
そうそう、あってるよ!ジニ係数はある地域内に住む人たちの貧富の格差を定量化するのに役立つんだけど、ジニ係数と併せてローレンツ曲線もセットに覚えておくと理解しやすいから、今日はジニ係数とローレンツ曲線について理解できるようにしていこう!
ローレンツ曲線とは?
ジニ係数もローレンツ曲線も、どちらとも「所得分配の不平等さ」を調べるために使うことができ、本質的には同じものになります。それでは何が違うのかというと、ジニ係数、ローレンツ曲線という言葉からもわかるように、ジニ係数は数値、ローレンツ曲線は図で不平等具合を表したものになります。公務員試験ではローレンツ曲線を使ってジニ係数を求めたりするので、まずはローレンツ曲線から見ていきましょう。
ローレンツ曲線とは、縦軸に所得の累積の比率、横軸に累積の人口比率をとる図において図示できる右上がりの曲線になります。

縦軸と横軸は、それぞれ累積の所得、人口比率をとりますが、ローレンツ曲線では、下位何%までで社会全体の何%の所得を得ているのかを見ることができます。例えば、上記の図の、横軸の人口の累積割合50%を見てください。この時、ローレンツ曲線を見ると縦軸の所得の累積比率は20%となっています。これは、この社会において下位50%の人々の所得を足し合わせても、全体の所得額の20%にしか満たないことを表しています。次に、横軸の人口の累積割合75%において、縦軸は50%となっています。これは、この社会において下位75%の人々の所得を足し合わせると全体の50%になるということを表しています。
ここから、社会の中で所得分配が平等になされていないことが分かります。なぜかというと、もし完全に平等な社会であれば、下位10%の人でも上位10%の人でも所得額が同じになるため、人口の累積割合10%の時点で所得の累積割合は10%となり、人口の累積割合20%なら所得の累積割合20%と、一定の割合で変化するためです。このような状況を完全平等な社会と言い、ローレンツ曲線は以下のように直線となります。

一方で、不平等の度合いが大きくなればなるほど、カーブが点Bに近い形のローレンツ曲線となります。
極端なケースでは以下のようにL字型のローレンツ曲線になります。この時、社会の中で1人のみが全ての富を独占し、その他の人々は所得がゼロということを表しています。このように、そのローレンツ曲線が直線OAに近ければ近いほど、その社会では不平等度合いが小さく、逆にローレンツ曲線がL字型に近ければ近いほど、その社会での所得分配は不平等であることを表します。

ジニ係数とは?
ジニ係数とは、ローレンツ曲線で表した不平等具合を数値化したものになります。ジニ係数はゼロから1までの値をとり、ゼロに近い値をとる場合は平等で、逆に1に近い値をとる場合は不平等となります。ジニ係数は、ローレンツ曲線を使って求めることができます。

ローレンツ曲線は、直線OAに近い曲線であればその社会での所得分配は平等に近く、逆にローレンツ曲線がL字型になればなるほど不平等具合が増すことを先ほど説明しましたが、これは直線OAとローレンツ曲線で囲ったXの面積が大きくなればなるほど不平等であるといえます。そこで、ジニ係数自体は以下のようにローレンツ曲線を使って求めることができます。
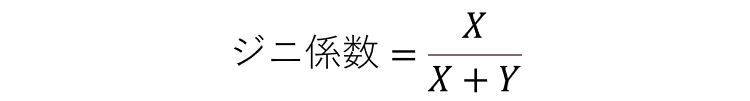
ジニ係数はつまり、Xの部分の面積を三角形OBAの面積で割ったものになります。もしローレンツ曲線が直線OAに沿った直線となった場合には、Xはゼロになるため、ジニ係数もゼロとなります。一方で、ローレンツ曲線がL字型の場合、面積Yの部分がなくなってしまうので、X/X=1となります。
実際に「世界のジニ係数 国別ランキング・推移」を見てみると、日本のジニ係数は0.34となっています。他の国を見てみると、例えばドイツは0.29、アメリカは0.39となっています。また、ランキングを見てみると1位、つまり不平等具合が高い国は南アフリカで0.62となっています。このデータを見て日本の不平等度合いが高いと思うか低いと思うかは個人の主観となると思いますが、最近の傾向として日本のジニ係数は上昇傾向、つまり所得格差が拡大しているようです。こういった知識面も公務員試験では出題されるので押さえておく必要があります。
ジニ係数の計算
最後に、公務員試験でよく出題される例題を見ていきたいと思います。
|
[例題] 3つの家計から成る社会を考える。それぞれの家計の所得は0円、1,000万円、2,000万円とする。この社会のジニ係数はいくつか。
|
[解法]
|
①ローレンツ曲線を作る。 ジニ係数を求める際には、ローレンツ曲線を実際に作って図にして考えてみると分かりやすくなります。設問に沿ってローレンツ曲線を作ると以下のようになります。
まず、公務員試験で実際に計算問題が出てきた場合、例題のように家計が3人など社会に存在する人が少なく世呈されていることが多いです。そのため、図の横軸は割合ではなく、累積人口の人数、縦軸は累積所得の額をとってローレンツ曲線を作ってみると分かりやすくなります。
すると、まず所得が一番低い人として、所得額0円の方が一人いるため、ローレンツ曲線の横軸の累積人口1人のところは、0円となります。次に、累積人口2人の部分は、所得0円と1,000万円をたしあわせるため、ローレンツ曲線は1,000万円のところを通ります。最後に累積人口3人のところは、3人の所得額の合計となるため、累積所得は3,000万円となり、上記のようなローレンツ曲線を作ることができます。 |

|
②各面積を求める。 次に、ジニ係数を求めるために必要なXと、Yの面積を求めます。Xの部分を直接求めることは難しいので、まずYの部分の面積を求め、三角形OBA(X+Y)からYの部分の面積を差し引くことによってXの面積も求めます。 (Yの面積)=(1×1,000×1/2)+{1×(1,000+3,000)×1/2}=2,500 (三角形OBAの面積)=3×3,000×1/2=4,500 まず、Yの部分の面積については、累計人口1から2までの間の面積と、2から3までの間の面積に分けて計算することができます。累計人口1から2までの間の面積は三角形の面積の公式を使い、累計人口2から3までの間の面積は、台形の面積の公式を使うと求めることができます。以上より、Xの面積も以下のように求めることができます。 (Xの面積)=4,500-2,500=2,000 |
|
③ジニ係数の式に当てはめる X部分の面積と三角形OBAの面積が分かったので、これらをジニ係数の式に当てはめれば答えにたどり着けます。 ジニ係数=2,000/4,500≒0.444… |
最後に
財政学は専門試験で出題されますが、ジニ係数の問題自体は教養試験に出題されることもあります。専門試験がない試験の場合にも出題される可能性は高いので、ぜひマスターできるようにしましょう!